量子计算入门内容总结

1. 根本常识

在起头正式进修量子计较之前，我们需要具有一些根基的物理学、数学和量子计较相关的根本常识。

1.1. 物理根本常识

传统计较机遵守典范物理学的物理定律，而量子计较机需要依靠量子力学中的一些重要概念来实现：

1. 态叠加道理 (Quantum superposition)：一个量子系统的量子态可所以多种分歧量子态的肆意一种，则它们的归一化线性组合也可以是其量子态，我们凡是称这类线性组合为叠加态。

2. 量子丈量 (Quantum measurement)：处于不异状态的量子系统被丈量后能够会获得完全分歧的成果，这些成果合适一定的几率散布。

3. 量子纠缠 (Quantum entanglement)：量子系统平分歧部分之间的丈量是相关联的。

在传统计较机中，1比特 (bit) 代表二进制中的一位数，即0或1；在量子计较中，我们经过 \mathinner{|0\rangle} 和 \mathinner{|1\rangle} 来暗示量子比特 (qubit)。物理意义上， \mathinner{|0\rangle} 代表一个原子的基态， \mathinner{|1\rangle} 代表一个原子中的激起态。经过上面所述的态叠加道理，我们可以晓得一个量子比特状态可以用以 \mathinner{|0\rangle} 和 \mathinner{|1\rangle} 为基向量的线性组合，即 \mathinner{|\psi\rangle}=a_{0}\mathinner{|0\rangle}+a_{1}\mathinner{|1\rangle} ，其中 a_{0}, a_{1} \in \mathbb{C}， |a_{0}|^{2} 和 |a_{1}|^{2} 用于暗示丈量“0”和“1”的几率，明显这里我们有 |a_{0}|^{2}+|a_{1}|^{2}=1 。

1.2. 数学根本常识

我们晓得一个了量子比特状态可以用以 \mathinner{|0\rangle} 和 \mathinner{|1\rangle} 为基向量的线性组合，自然我们便可以引入量子比特的矩阵表达式，在这里我们有 \mathinner{|0\rangle}= \begin{bmatrix} 1\\ 0 \end{bmatrix} ， \mathinner{|1\rangle}= \begin{bmatrix} 0\\ 1 \end{bmatrix} ，是以，对于一个量子比特状态 \mathinner{|\psi\rangle}=a_{0}\mathinner{|0\rangle}+a_{1}\mathinner{|1\rangle} ，我们可以将它暗示成 a_{0}\mathinner{|0\rangle}+a_{1}\mathinner{|1\rangle}= \begin{bmatrix} a_{0}\\ a_{1} \end{bmatrix} 。针对左矢 (bra)，我们可以把他写成一个行向量的形式，例如假定我们有 \mathinner{|\psi\rangle}= \begin{bmatrix} a_{0}\\ a_{1} \end{bmatrix} ，那末它所对应的对偶向量 (dual vector) 为 \mathinner{\langle \psi|}= \begin{bmatrix} a_{0}^{*} & a_{1}^{*} \end{bmatrix} 。对于左右矢的运算，我们一样需方法会内积 (inner product) 和外积 (outer product) 的算法：假定我们有 \mathinner{|\psi\rangle}= \begin{bmatrix} a\\ b \end{bmatrix} ， \mathinner{|\phi\rangle}= \begin{bmatrix} c\\ d \end{bmatrix} ，那末我们便可以获得： \mathinner{\langle\psi \mid \phi\rangle} \equiv \mathinner{\langle\psi \| \phi\rangle}= \begin{bmatrix} a^* & b^* \end{bmatrix} \begin{bmatrix} c\\ d \end{bmatrix}=a^{*}c+b^{*}d ， \mathinner{|\psi\rangle\langle\phi|} = \begin{bmatrix} a\\ b \end{bmatrix} \otimes \begin{bmatrix} c^* & d^* \end{bmatrix}= \begin{bmatrix} ac^* & ad^*\\ bc^* & bd^* \end{bmatrix} 。

1.3. 量子计较根本常识

1.3.1 布洛赫球的表达形式

由于复数可以暗示成极坐标的形式，是以我们有 \mathinner{|\psi\rangle}=a_{0}\mathinner{|0\rangle}+a_{1}\mathinner{|1\rangle}=|a_{0}|e^{i \theta_{0}}\mathinner{|0\rangle}+|a_{1}|e^{i \theta_{1}}\mathinner{|1\rangle} ，经过对这个式子的重新整理我们可以获得：\mathinner{|\psi\rangle}=|a_{0}|e^{i \theta_{0}}\mathinner{|0\rangle}+|a_{1}|e^{i \theta_{1}}\mathinner{|1\rangle}=e^{i \theta_{\text{global}}}\left(\cos{\frac{\theta_{B}}{2}}\mathinner{|0\rangle}+\sin{\frac{\theta_{B}}{2}}e^{i \phi_{B}}\mathinner{|1\rangle}\right) ， \phi_{B}=\theta_{1}-\theta_{0} 。对于单量子比特我们凡是疏忽 \theta_{\text{global}} ，量子系统的状态经过布洛赫角度 (即 \theta_{B}, \phi_{B}) 来暗示，因而我们可以获得： \mathinner{|\psi\rangle}=a_{0}\mathinner{|0\rangle}+a_{1}\mathinner{|1\rangle} \rightarrow \cos{\frac{\theta_{B}}{2}}\mathinner{|0\rangle}+\sin{\frac{\theta_{B}}{2}}e^{i \phi_{B}}\mathinner{|1\rangle} 。在布洛赫球 (Bloch sphere) 中可以暗示成以下图所示的图像：

1.3.2 单量子比特上的量子操纵

我们凡是可以经过量子操纵 (Quantum operations)将量子系统的状态转换成一个新的状态，即 \mathinner{|\psi'\rangle}=U\mathinner{|\psi\rangle} ，这里的 U 即代表一个量子操纵。这样可以转换原有量子系统状态的量子操纵，我们凡是也称它们为量子门 (Qubit gates)，常见的三种门别离为 X 门， Y 门和 Z 门，它们可以经过泡利矩阵的形式来表达；除此之外，我们还有 I 门， S 门，T 门， H 门和 R 门，它们也可以经过矩阵的形式表达。

假定在量子法式中我们有一组操纵序列，从左往右依次为 X 门， Y 门和 Z 门，那末对于这样的一组操纵序列，我们可以按照每一个步调对 \mathinner{|\psi\rangle} 停止转换，以下图所示：

将这三步连系起来我们可以写成 \mathinner{|\psi (t=3)\rangle}=ZYX\mathinner{|0\rangle} ，留意这里的顺序不能出现毛病！

1.3.3 双量子比特上的量子操纵

经过前面的进修我们晓得，假如我们有两个量子比特，那末我们可以经过求它们的张量积 (tensor product)来求得一个双量子比特的状态，即假如我们有 \mathinner{|\psi\rangle}=a\mathinner{|0\rangle}+b\mathinner{|1\rangle} 和 \mathinner{|\phi\rangle}=c\mathinner{|0\rangle}+d\mathinner{|1\rangle} 这两个量子比特的状态，那末双量子比特的状态应当为 \mathinner{|\psi\rangle} \otimes \mathinner{|\phi\rangle} =ac\mathinner{|00\rangle}+ad\mathinner{|01\rangle}+bc\mathinner{|10\rangle}+bd\mathinner{|11\rangle} 。将这个双量子比特的状态简写为 \mathinner{|\psi\rangle}=a\mathinner{|00\rangle}+b\mathinner{|01\rangle}+c\mathinner{|10\rangle}+d\mathinner{|11\rangle} ，我们可以晓得，假如第一位量子比特丈量出来的成果为“0”，那末我们只需要保存 \mathinner{|00\rangle} 和 \mathinner{|01\rangle} 这两个状态，并将它们重整化 (renormalize) 以获得一个新的状态： \displaystyle \mathinner{|\psi'\rangle}=\frac{a\mathinner{|00\rangle}+b\mathinner{|01\rangle}}{\sqrt{|a|^{2}+|b|^{2}}} ；类似的，假如第一位的量子比特丈量出来的成果为“1”没，我们重整化以后也会获得一个新的状态： \displaystyle \mathinner{|\psi'\rangle}=\frac{c\mathinner{|10\rangle}+d\mathinner{|11\rangle}}{\sqrt{|c|^{2}+|d|^{2}}} 。

对于双量子比特上的单量子门操纵，我们顺从类似的操纵顺序，即从左往右，从上往下（大概从下往上）依次操纵，例如对于下图中的例子而言，我们挑选先对第二个量子比特停止从左往右的操纵，以后再对第一个量子比特停止从左往右的操纵，和从左往右不成以变动纷歧样的是，对于双量子比特上的量子操纵，高低顺序可以停止颠倒，对于这个例子而言，即我们可以先辈行对第一个量子比特的操纵，然后再停止第二个量子比特的操纵，即也可以写成： \mathinner{|\psi (t=2)\rangle}=X_{2}H_{2}Y_{1}H_{1}\mathinner{|0\rangle} 。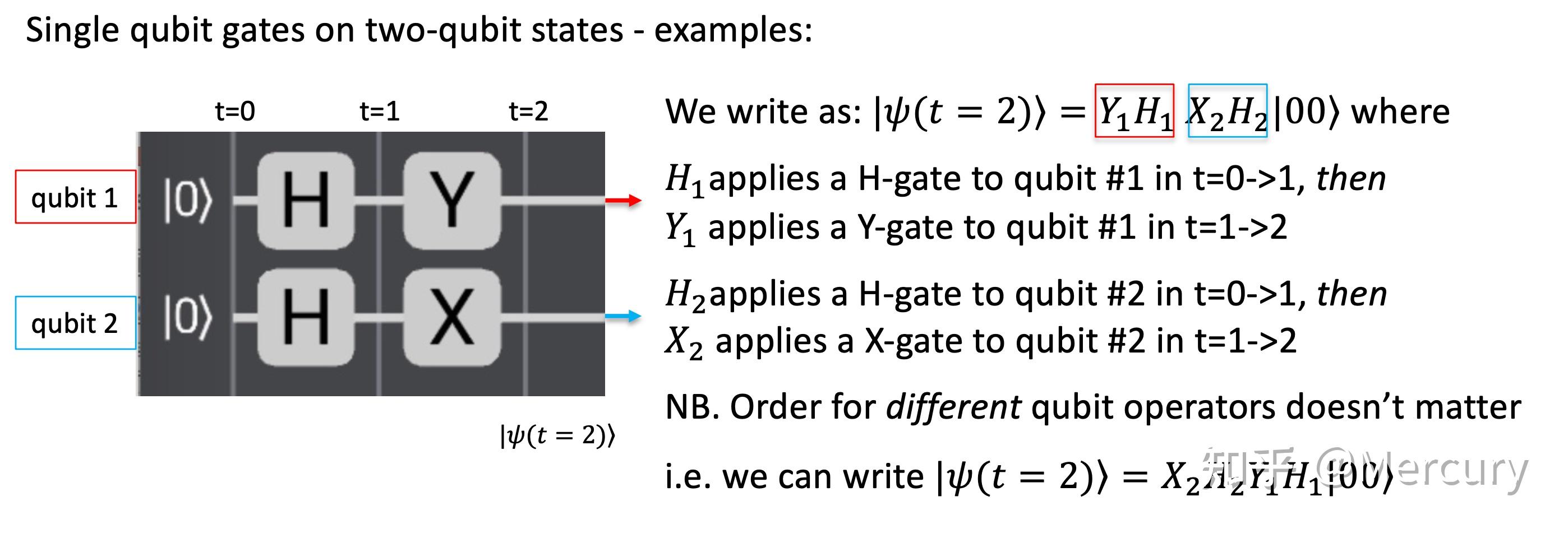

除了单量子门之外，我们还有一些常见的，极为重要的双量子门，它们包括 CNOT 门， CZ 门和 SWAP 门，它们每个都有纷歧样的功用。

对于 CNOT 门来说，它一般触及两个量子比特，别离为控制比特 (control qubit) 和方针比特 (target qubit)，当控制比特为 \mathinner{|0\rangle} 时，方针比特则连结原状态；当控制比特为 \mathinner{|1\rangle} 时，方针比特则停止反转，例如对于一个双量子比特状态 \mathinner{|\psi\rangle}=a\mathinner{|00\rangle}+b\mathinner{|01\rangle}+c\mathinner{|10\rangle}+d\mathinner{|11\rangle} 来说，经过 CNOT 门的操纵以后，它会酿成 \mathinner{|\psi'\rangle}=a\mathinner{|00\rangle}+b\mathinner{|01\rangle}+d\mathinner{|10\rangle}+c\mathinner{|11\rangle} 。 CZ 门一般也是触及两个量子比特，当控制比特为 \mathinner{|1\rangle} 时，方针比特的相位会停止反转 (操纵 Z 门)，例如对于一个双量子比特 \mathinner{|\psi\rangle}=a\mathinner{|00\rangle}+b\mathinner{|01\rangle}+c\mathinner{|10\rangle}+d\mathinner{|11\rangle} 来说，经过CZ 门的操纵以后，它会酿成 \mathinner{|\psi'\rangle}=a\mathinner{|00\rangle}+b\mathinner{|01\rangle}+c\mathinner{|10\rangle}-d\mathinner{|11\rangle}； SWAP 门一般也是触及两个量子比特，它的感化首要为交换两个量子比特的状态，即对于一个双量子比特 \mathinner{|\psi\rangle}=a\mathinner{|00\rangle}+b\mathinner{|01\rangle}+c\mathinner{|10\rangle}+d\mathinner{|11\rangle} 来说，经过 SWAP 门的操纵以后，它会酿成 \mathinner{|\psi'\rangle}=a\mathinner{|00\rangle}+c\mathinner{|01\rangle}+b\mathinner{|10\rangle}+d\mathinner{|11\rangle} 。

在操纵进程中，我们偶然辰会碰到量子系统的纠缠态 (entangled state)，在量子计较中，我们对于纠缠态的界说为不成份离的状态。我们常说、常见的一种纠缠态为贝尔态 (Bell state)，它可以写成 \displaystyle \frac{\mathinner{|00\rangle}+\mathinner{|11\rangle}}{\sqrt{2}} 的形式，很明显我们不能将这个式子写成两个量子系统状态的张量积。

在一般的量子计较模拟系统中，我们一般会自动获得纠缠熵 (entanglement entropy) 的值，一样我们也可以经过计较得出，即 H=-\lambda_{1}\log_{2}(\lambda_{1})-\lambda_{2}\log_{2}(\lambda_{2}) ，对于双量子比特而言，最大的纠缠熵即为1比特。

1.3.4 多量子比特上的量子操纵

我们经常会需要斟酌多量子比特上的量子操纵，我们把这样的一组量子比特称为量子寄存器 (quantum register)。

在多量子比特上的量子操纵中，我们常用的一个量子门叫做Toffoli门，它具有三路输入和三路输出，假如前两个量子比特为 \mathinner{|1\rangle} ，那末第三个量子比特则停止反转，例如我们有一个三量子比特 \mathinner{|\psi\rangle}=a\mathinner{|000\rangle}+b\mathinner{|001\rangle}+c\mathinner{|010\rangle}+d\mathinner{|011\rangle}+e\mathinner{|100\rangle}+f\mathinner{|101\rangle}+g\mathinner{|110\rangle}+h\mathinner{|111\rangle} ，经过Toffoli门的操纵后，它会酿成 \mathinner{|\psi'\rangle}=a\mathinner{|000\rangle}+b\mathinner{|001\rangle}+c\mathinner{|010\rangle}+d\mathinner{|011\rangle}+e\mathinner{|100\rangle}+f\mathinner{|101\rangle}+h\mathinner{|110\rangle}+g\mathinner{|111\rangle} 。

2. 从传统算法到量子算法

量子算法是一种专门用于量子计较机处理计较题目标算法，那末我们为什么不在量子计较机上利用传统算法呢？首先是由于量子计较机的道理和传统计较机有本质上的分歧，我们需要按照量子力学中展现出的特征，如纠缠，叠加等专门设想较法；其次就是假如我们在传统计较机上运转量子算法，那末能够只会进步 C_{e} ，而不是 f(n) 。今朝已经稀有百个量子算法被设想出来，我们将鄙人面的内容中先容最为成熟以及广为人知的几个。

2.1. Deutsch-Jozsa算法

首要处理的题目：经过预言机判定输入的函数 f 是常函数 (constant function)还是平衡函数 (balanced function)。

首先我们来界说一下什么是常函数战争衡函数，我们将常函数界说为函数值一定的函数，以下表所示，不管 f(x) 中的 x 取1或0，常函数的函数值总为一个牢固的常数；同时我们将平衡函数界说为函数值出现频次分歧的函数，以下图所示，不管 f(x) 中的 x 取1或0，平衡函数的函数值总会出现一次1和一次0。

对于单量子比特的常函数战争衡函数，我们可以设想以下的电路停止测试：

Deutsch-Jozsa算法的具体结构图以下所示，我们可以按照分歧的题目对下面的 U_{f} 停止替换。对于一个常函数而言，我们一定会丈量出“0”，而对于一个平衡函数而言，我们一定会丈量出“1”。

扩大到多量子比特的情况，假如我们在输出寄存器中只能获得0，那末这个函数便可以判定为常函数，假如我们获得任何除0之外的值，那末这个函数便可以被判定为平衡函数。

在传统算法中，我们计较这类题目凡是需要斟酌 (\frac{2^{n}}{2})+1=\mathcal{O}(2^{n}) 种情况，而在量子算法中，我们只需要完成 1=\mathcal{O}(1) 次操纵便可以完成检验，但是今朝并没有找到DJ算法的现适用处。

2.2. Simon算法

首要处理的题目：对于1个给定的2-to-1函数 f ，我们有 f(x)=f(x \oplus a) ，找到 a 的值。

Simon算法的具体结构图以下图所示，经过丈量出的 y 值 ( y 值为最上面输出寄存器的值)，我们有 a \cdot y=0 \text{ mod }2，例如对于三量子比特来说，假定我们丈量出的值别离为：001，110，111， a 是一个三比特的数字 (a_{1}, a_{2}, a_{3}) ，那末我们便可以列出这样的方程组： a_{3}=0, a_{1}+a_{2}=0, a_{1}+a_{2}+a_{3}=0 ，经过解这样一个三元一次方程获得 a=(a_{1}, a_{2}, a_{3}) 的值。一样，今朝并没有找到Simon算法的现适用处。

2.3. Shor算法

首要处理的题目：找出这个函数 f(x)=a^{x} \text{ mod } N 的周期。

Shor算法现实上也是QPE电路的一个利用，具体的Shor算法结构图以下图所示：

首先在经过 H 门以后，上面输出寄存器的状态就酿成了： \displaystyle \mathinner{|\psi\rangle}=\frac{1}{\sqrt{2^{n}}}\sum^{N-1}_{x=0}\mathinner{|x\rangle}\mathinner{|1\rangle} ，第二步我们停止 \mathinner{|a^x \text{ mod } N\rangle} 的运算，例如假定我们在上面的输出寄存器中包括 x=101_{2} ，同时 a=2, N=15 ，我们就要停止：首先从1起头，以后乘上 a^{1}=2^{1}=2 ，即给出了 2 \text{ mod }15 ；接下来我们不斟酌 a^{2} ，我们间接看 a^{4}=2^{4}=16 ，即给出了 32 \text{ mod } 15 的值，用标记暗示即为 \displaystyle \mathinner{|\psi\rangle}=\sum_{x}\mathinner{|x\rangle}\mathinner{|a^x \text{ mod } N\rangle} 。接下来我们在底部的存储器丈量出了某一个具体的值，这样全部量子法式的状态就会塌缩成一切满足条件的 x 。

经过以后的量子傅立叶变更，我们停止丈量，可以获得一个肆意的 \displaystyle m=k\frac{2^{n}}{r} ，这里的 n 是上面寄存器中包括的量子比特数， r 则为需要我们寻觅的周期。经过对 \displaystyle \frac{k}{r}=\frac{m}{2^{n}} 停止连分数法，我们可以获得一个偶数 r 的值。最初经过 \displaystyle (a^{\frac{r}{2}}+1)(a^{\frac{r}{2}}-1) 获得 N 的 gcd 。

2.4. Grover算法

首要处理的题目：非结构化搜索题目 (unstructured search problems)

具体的Grover算法结构图以下图所示，具体来说一个Grover算法是由 n 个Grover迭代组成的，一个Grover迭代可以由一个预言机和一个反转组成。预言机的目标主如果为了标志成果，并将它的振幅的标记停止翻转；反转的目标主如果为了放大成果的振幅，将之前经过预言机的成果对着均匀值停止反转，例以下图中演示的步调那样。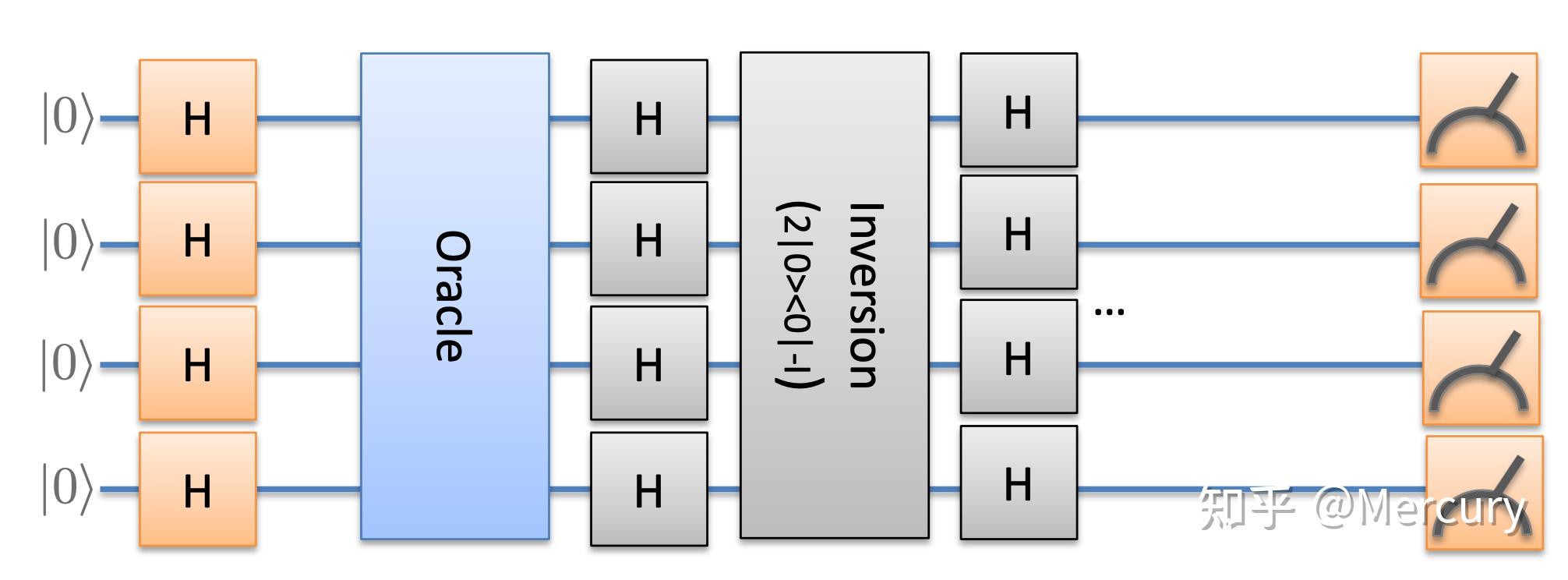

那末我们在一个算法里到底需要几多个Grover迭代呢？这个成果取决于题目中解的个数。假定我们一共需要处置 N 种情况，一共有 M 个解，那末我们可以获得 \displaystyle \sin{\theta}=\frac{\sqrt{M}}{\sqrt{N}} ，从多少上去了解这个 \theta ，就是第一次经过预言机，向下翻转的角度（以下图所示）。对于比力小的 \theta 来说， \displaystyle \theta=\sin{\theta}=\frac{\sqrt{M}}{\sqrt{N}} 。在经过 k 次Grover迭代后，我们有： \displaystyle (2k+1)\theta=\frac{\pi}{2} 。

那末Grover迭代中具体的量子法式是什么样的呢？假定我们有一个解是 4=\displaystyle \mathinner{|100\rangle} ，我们可以经过利用 X 门和 CZ 门来停止操纵，具体来说，针对一个为 4=\displaystyle \mathinner{|100\rangle} 的解，我们可以有以下的Grover迭代：

2.5. QAOA算法

QAOA算法的先容可见这篇文章里的内容，QAOA算法一样可以被用来处理投资组合优化等类似的优化题目中。

3. 量子计较在密码学中的利用

3.1. RSA加密算法

3.1.1. 公钥与私钥的发生

首先第一步随意挑选两个大的素数 p 和 q ，且 p \neq q ，求得 N=pq ；第二步按照欧拉函数 (Euler's totient function)，计较出 r=\phi(N)=\phi(p) \times \phi(q)=(p-1)(q-1) ；第三步挑选一个小于 r 的整数 e ，使 e 与 r 互质 (一般我们取37)，并求得 e 关于 r 的逆模元，命名为 d ( ed \equiv 1 \text{ mod } \phi(N) )，经过扩大欧几里得算法，我们可以获得 \text{gcd}[e, \phi(N)]=ex+\phi(N)y ，最初我们获得 d=x 。在这里 (N,e) 是公钥， (N,d) 是私钥。假如Alice希望经过不成靠的媒体接管Bob的私人信息，那末Alice可以将公钥 (N,e) 传给Bob，而将她的私钥 (N,d) 藏起来。

3.1.2. 加密消息

假定Bob假如想给Alice发送消息 M ，他可以经过以下的公式将 M 停止加密： C=M^{e} \text{ mod } N 。

3.1.3 解密消息

Alice在接收到Bob的加密信息后便可以用手中的密钥来停止解密： M=C^{d} \text{ mod } N 。

3.2. 量子密钥分发 (QKD)

量子密钥分发首要遵守以下几个步调：第一步：Alice挑选肆意的基来对一个量子比特停止编码，并将编码后的量子比特发给Bob；第二步Bob经过肆意的基对收到的信息停止丈量；第三步Alice和Bob公然公布他们利用丈量的基，假如纷歧样就间接放弃继续判定，假如一样就停止判定：假如他们获得的成果纷歧样，那末中心能够存在窃听者，假如成果一样，那末这部分便可以被用来看成密钥。

在量子计较中我们存在两种基：z基和x基。例如Alice假如用x基来暗示 \mathinner{|1\rangle} ，Alice发给Bob的消息即为 \mathinner{|-\rangle} ，Bob在接收到信息后假如一样用x基停止解密，那末他就会获得 \mathinner{|1\rangle} ；类似的，假如Alice假如用z基来暗示 \mathinner{|1\rangle} ，Alice发给Bob的消息即为 \mathinner{|1\rangle} ，Bob在接收到信息后假如一样用z基停止解密，那末他就会获得 \mathinner{|1\rangle} 。假如Bob利用了毛病的基停止解密，那末他将会获得一个叠加态，丈量出 \mathinner{|1\rangle} 的几率为50%，丈量出 \mathinner{|0\rangle} 的几率也为50%。

现在假定在Alice和Bob传递信息的进程中有窃听者的存在，会有25%的几率让Bob即使利用了正确的基照旧得不到正确的信息。即：假如Bob利用了和Alice不异的基，但丈量出的成果纷歧样，那末就判定能够存在窃听者。

4. 量子机械进修

机械进修的首要分类可以分红监视进修 (Supervised Machine Learning) 和无监视进修 (Unsupervised Machine Learning)两种：例如神经收集 (Neural Networks)，深度进修 (Deep Learning)，支持向量机 (SVMs)等都为监视进修；主成份分析，SVD等为非监视进修；这里我们首要摸索一下主成份分析的内容

4.1. 主成份分析 (Principal Component Analysis)

主成份分析，望文生义，我们需要发现数据集的主成份。主成份分析的优点是它明显下降了数据维度，但是低维数据中照旧包括原始数据中的重要特征。主成份分析的工作步调首要分红以下几步：第一步是数据集的标准化；第二步为计较协方差矩阵；第三步为找出主成份：即协方差矩阵的特征向量和特征值；第四步为对原数据集的降维。

首先是数据集的标准化，数据集的标准化凡是需要我们用数据的均匀值和标准差来对数据停止调剂，这里我们的公式为 \displaystyle \text{Adjusted data}=\frac{\text{original data}-\text{mean}}{\text{standard deviation}} 。第二步是计较协方差矩阵 \begin{bmatrix} Cov(X,X) & Cov(X,Y)\\ Cov(Y,X) & Cov(Y,Y) \end{bmatrix} 。第三步是求出特征值和特征向量，对于一组 n 维的数据，我们可以获得一个 n*n 的协方差矩阵，即我们可以获得 n 个特征值和特征向量。最初一步是找到最高的 r 个特征值，并将 n 维的数据下降至 r 维。

4.2. 量子主成份分析 (Quantum Principal Component Analysis)

为了找到量子电路中的主成份，我们第一步需要找到量子系统状态的协方差矩阵，这个我们经过数据向量来完成，即 \displaystyle \overrightarrow{x_{j}} \rightarrow \mathinner{|x_{j}\rangle}=\sum_{i}x^{i}_{j}\mathinner{|i\rangle} ；第二步我们为每个随机挑选的状态预备多个副本，以便于具有多个协方差矩阵副本；第三步我们针对协方差矩阵状态的每个副本停止自然指数的 SWAP 门操纵 (基于欧拉公式)，即 e^{-i \operatorname{SWAP} \Delta t}=\cos (\Delta t) \mathbb{I}-i \sin (\Delta t) \mathrm{SWAP} ；第四步我们利用QPE算法来决议特征值，以下是首要的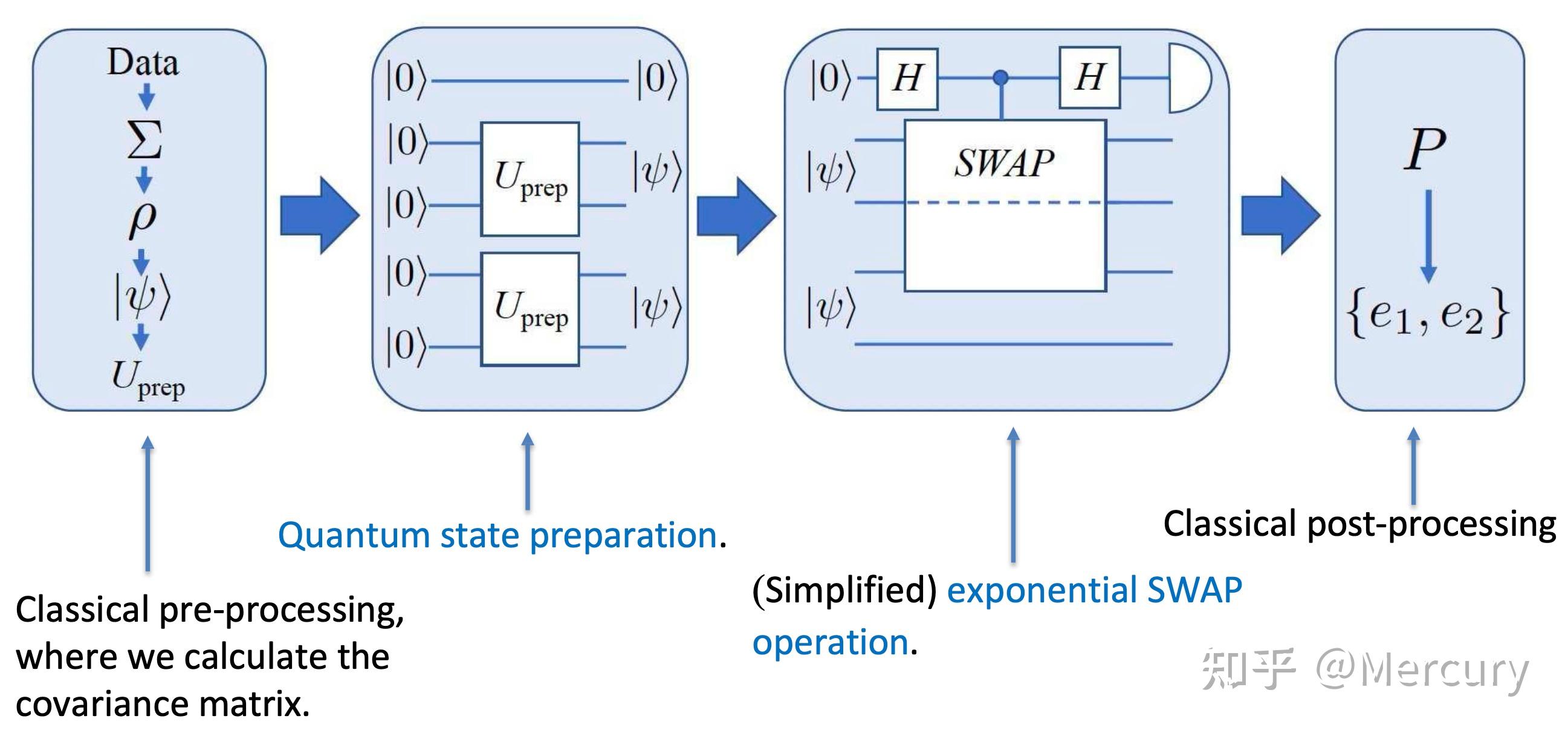结构图：

Reading List:
The lecture notes for 2023 Semester 2 University of Melbourne second year physics subject: Elements of Quantum Computing, on which my notes mainly based.