身边的微分方程(7)：一文读懂薛定谔方程

| 2022-2-27 21:49 阅读 1436 评论 20

本文为“身旁的微分方程”系列第7篇。难度提醒：★★★★★

若想领会本系列及本专栏其他文章，请收藏目录：

或按下文方式关注本专栏：

0) 开篇语

本文中，我们将迎来本系列的一位VIP，它是主宰微观天下运转纪律的根基法典、更是开创二十世纪光辉物资文化的第一鞭策。

即使不昂首看本文题目，我们也能猜到，本文要进场的这位VIP，就是薛定谔方程：

$\small \text i\hbar\frac{\partial }{\partial t}\psi=-\frac{\hbar^2}{2m}\nabla^2\psi+V\psi$

关于它如作甚现代文化带来的一个个神迹，我们将在后续的几篇文章里渐渐体味。

在此之前，我们需要先来参悟一下方程自己的意义。

否则，等我们自虐般地解完一堆分歧约束态的薛定谔方程以后，能够仍然不晓得自己在干啥。

而为了到达循序渐进的结果，我们将薛定谔方程的参悟的进程，由具象到笼统、拆成两个题目往返答：

适用主义之问：求解薛定谔方程能获得什么有用信息？
猎奇心害死薛定谔的猫之问：薛定谔方程自己的寄义是什么？

1) 求解薛定谔方程能获得什么？

在中学物理中，我们就晓得，一个原子核的核外电子的能量常常不能持续取值，而只能处在一些分立的能量值上面，这些分立的能量值叫作电子的能级(Energy Level)。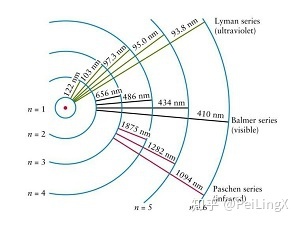

当我们在化学课中会商一个元素化学性质的第一性道理时，大概当我们在半导体物理中会商导带、禁带等决议半导体材料性能的关键身分时，实在本质上就是在间接或间接会商原子核外电子的能级散布。

而这些能级散布的信息，正是薛定谔方程给出来的。

换句话说，求解薛定谔方程能获得的最重要的信息，就是一个系统中答应存在的能级。

假如先放下全部方程的物理意义不谈，仅仅满足于“获得能级信息”这个适用主义的目标，那末这个求解进程了解起来并不难，我们顿时就能体验一番。

先来瞥一眼薛定谔方程：

$\small \text i\hbar\frac{\partial }{\partial t}\psi=-\frac{\hbar^2}{2m}\nabla^2\psi+V\psi$

此处：

$\small \text i$ 即虚数单元；

$\small \hbar=\frac{h}{2\pi}$ ， $\small h$ 即普朗克常数，而 $\small \hbar$ 称为约化普朗克常数；

$\small \bm\nabla=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)$ ，即梯度算子；

$\small V=V(x,y,z)$ ，是系统中的势能散布，取决于具体的物理情形；

$\small \psi=\psi(x,y,z,t)$ ，即名声在外的波函数(Wave Function)。

而为了方便会商，我们无妨先将方程简化为一维情形，此时梯度算子退化为对 $x$ 坐标的偏导数，方程简化为：

$\small \text i\hbar\frac{\partial }{\partial t}\psi=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\psi+V\psi$

按照我们在前面几课中对线性偏微分方程的熟悉，我们晓得，要求解这样一个方程，标准做法是先分手变量，获得关于坐标和关于时候的两个自力的函数，记为：

$\small \psi(x,t)=\phi(x)T(t)$

这样，方程就化为：

$\small \text i\hbar \phi T'=-\frac{\hbar^2}{2m}T\phi ''+V\phi T$

双方同时除以 $\small \phi T$ ，得：

$\small \text i\hbar \frac{T'}{T}=-\frac{\hbar^2}{2m}\frac{\phi ''}{\phi }+V$

我们无妨令方程双方同时即是某个常数：

$\small \text i\hbar \frac{T'}{T}=-\frac{\hbar^2}{2m}\frac{\phi ''}{\phi }+V=E$

这样就能将两个自力的方程别离求解了。

而按照之前求解弦振动和热传导方程的经历，我们需要重点关注的，凡是是坐标的方程：

$\small -\frac{\hbar^2}{2m}\frac{\phi ''}{\phi }+V=E$

为了方便前面的会商，我们将双方同时乘以 $\small \phi$ ，这样方程化为：

$\small -\frac{\hbar^2}{2m}\phi ''+V\phi =E\phi$

这个方程叫作定态薛定谔方程(它也是我们会商薛定谔方程意义的关键 )。

回首本系列之前的文章中求解弦振动方程和热传导方程的经历，我们可以猜到：

假如限制了鸿沟条件，那末我们凡是会获得这个方程的一组特解序列 $\small \phi _n(x),\ n\in\mathbb{Z}$ ，而每个特解会对应一个常数值 $\small E_n$ ，满足方程：

$\small -\frac{\hbar^2}{2m}{\phi_n}''+V\phi_n=E_n\phi_n$

这里获得的常数序列 $\small \{E_n\}$ ，就是粒子能量答应出现的取值，也就是能级。

这里顺便说一句，一个系统里答应的能级 $\small E_n$ ，在量子力学中被称作能量的本征值(Eigen Value)，请记着这个词，它是我们了解方程物理意义的关键。

到这里，用薛定谔方程寻觅能级的进程就说完了。

看起来能否是很简单？我们仅仅挪用一下已经在前面的课程中练过手的分手变量法，就能解出答应出现的能级取值，这完全部验不到烧脑的感受啊……

可是别忘了，我们在这里仅仅是对求解步调做了一个简单先容，而并没有实在地履历在具体的势能条件下求解 $\small E_n$ 的进程。

相信我，等前面我们给出了具体的势能函数 $\small V(x)$ ，真正脱手求解的时辰，就会发现光阴静好都是假象。实在情况是，哪怕面临的是一切元素中最简单的氢原子系统，求解进程城市让我们疾苦到思疑人生。

但不管怎样样，假如我们不去纠结“为什么薛定谔方程解出来的 $\small E_n$ 就是我们要找的能级”之类的深条理题目，仅仅就功利主义的目标而言，了解到这一步，便可以进入具体的物理场景中求解薛定谔方程(虽然很疾苦 )、去见识那些改变人类历史进程的神迹了。

不外，作者相信，本文的读者不会宁愿就此打住，由于我们对于薛定谔方程的困惑实在太多：

比如波函数 $\small \psi$ 以及特解序列 $\small \phi_n$ 的物理意义是什么？又比如为什么系统答应的能级 $\small E_n$ 必须经过求解薛定谔方程来获得？

这两个题目标背后，实在也就是我们将要回答的第二个题目：

猎奇心害死薛定谔的猫之问：薛定谔方程自己的寄义是什么？

假如要用两句话往返答这个题目，我们可以说：

定态薛定谔方程就是典范力学能量关系：

$\small E=\frac{1}{2}mv^2+V=\frac{p^2}{2m}+V$

的量子版本。

而完整的薛定谔方程也可以看做牛顿第二定律的量子版本。

可是同学们要问了：这些方程的形式和典范力学看起来完全不像啊，怎样把它们联系起来呢？

在回答这个题目之前，我们还得追溯到一个更底子的题目：

进入量子力学天下的正确姿势是怎样的？

能够……是这样的？

2) 进入量子力学的正确姿势

我们晓得，在典范力学中，描写一个物理工具的状态时，我们用的是具体的、可以丈量的力学量(如位置、速度、动量、能量等 )。

而在量子力学中，一个物理工具或系统的状态，只需要用一个笼统的工具来描写，它叫做“态矢量 (State Vector)”，也就是我们凡是说的“量子态”。

(比如薛定谔的猫那种既生又死的状态就是态矢量的一个虚拟的、可是很直观的版本…… )

而这个笼统的态矢量有一种定量化的、可用于计较的表述方式，这正是波函数 $\psi(x,t)$

固然，有同学会很猎奇：一个函数怎样和一个被称作“矢量”的玩意儿联系起来？

这个我们前面再来体味。

现在我们来关注一个更重要的题目：

在量子力学中，我们熟悉的典范力学量信息被扔到那里去了？

究竟，宏观天下与微观天下不是割裂的，所以，典范力学中能获得的信息，量子力学中也必须包括。

这个题目标答案也不难猜到：

典范力学量的信息固然应当都包括在波函数傍边。

不外，这类说法还不够正确，更正确的说法是：

典范力学量的信息都以几率形式被包括在波函数傍边。

换句话说，波函数不是一个具体的物理量，但它包括了一切典范力学量的几率信息。

这样一来，从字面上来说，波函数 $\psi$ 的物理意义就清楚了：

它是一个包括了一切典范力学量几率信息的笼统物理量“态矢量”的具体化身。

(更正确地说，是在“坐标表象”下的具体化身，但这里我们不用去关注什么是“坐标表象”，有爱好晓得的同学可以关注本专栏另一个深度科普系列：从线性代数到量子力学)

那末具体怎样包括这些几率信息呢？

相信本文的读者都听说过薛定谔的猫吧，我们先用它来做一个不松散的说明。

我们晓得，在这个思惟尝试中，有一个盒子里装了三样工具：

一颗能够发生衰变的粒子、一台可以被粒子的衰变触发的杀猫神器、和一只万年网红猫。

当我们不翻开盒子时，对于盒子里面的观察者而言，粒子的衰变状态就是一个不肯定的状态，响应地、猫就处于一种“既生又死”的叠加态。

这类叠加态，就是一个典型的(虽然是虚拟的 )态矢量，究竟上，我们可以像向量的线性组合一样，将它暗示成向量叠加的形式：

$\left|\psi\right>=a_L\left|L\right>+a_D\left|D\right>$

这里我们采用的是一种叫做“狄拉克标记”的记法，其中 $\left|\psi\right>$ 就是描写“既生又死叠加态”的态矢量，而 $\left|L\right>$ 暗示观察到活猫的“活猫态”， $\left|D\right>$ 暗示观察到死猫的“死猫态”。

将它暗示成多少直观，就是这个样子：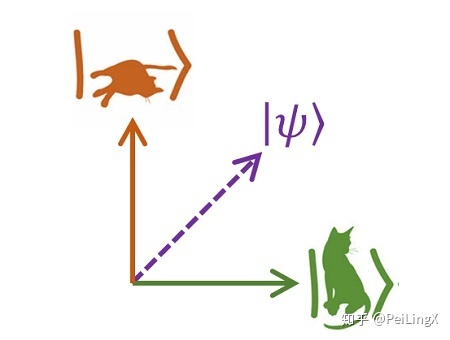

也就是说，当我们不去观察猫时，猫现实所处的状态，是“活猫态” $\left|L\right>$ 和“死猫态” $\left|D\right>$ 的线性叠加，这在典范物理中不成能存在的状态，恰正是量子力学的最大特征。

现在我们来说说几率信息：

适才我们看到，猫的态矢量的线性叠加关系中，有两个叠加系数 $a_L,a_D$ ，这两个系数就包括了几率信息。

具体说来，就是当我们翻开盒子观察猫的死活时，猫的状态会随机坍缩到“活猫态”和“死猫态”傍边的一个，坍缩到“活猫态”的几率是 $\left|a_L\right|^2$ ，而坍缩到“死猫态”的几率是 $\left|a_D\right|^2$

这就是态矢量包括几率信息的道理。

我们来看两个实在的例子。

3) 几率信息与本征态

第一个例子，是我们在很多量子力学科普书上都看到过的，波函数的统计诠释：

一个粒子的波函数的模方 $|\psi(x,y,z,t)|^2$ ，暗示 $t$ 时辰在 $(x,y,z)$ 处找到这个粒子的几率密度。

这句话就描写了波函数若何包括粒子位置的几率信息，前面的课程中，我们会看到它给我们带来的益处。

不外，位置究竟只是众多力学量中的一个，我们还要关注其他的力学量。

虽然其他力学量的几率信息不再像位置的几率信息那末明显，但我们仍然能找到它们。

比如我们接下来要说的第二个例子，也是我们最关注的能量。

在前面临薛定谔方程求解进程的描写中，我们晓得，经过度手变量，求解关于坐标的阿谁定态薛定谔方程，我们能获得特解序列 $\phi_n(x)$ 以及响应的能级序列 $E_n$ 。

而粒子处于某个能级的几率，就是经过特解序列 $\phi_n(x)$ 来计较的，我们顿时来看。

类比弦振动方程和热传导方程，我们晓得，假如给定了薛定谔方程的初始条件 $\psi(x,0)$ ，那末 $\psi(x,0)$ 可以暗示成 $\phi_n(x)$ 的级数和形式，即：

$\psi(x,0)=\sum_n{c_n\phi_n}$

而这里的系数 $c_n$ 的模方 $|c_n|^2$ 就代表了能量的几率信息，说得具体一点，就是：

对于一个初始状态处于 $\psi(x,0)$ 的粒子，当我们去丈量它的能量时，测得它处在能级 $E_n$ 上的几率为 $|c_n|^2$ 。

也就是说，在寻觅能量的几率信息时，特解序列 $\phi_n(x)$ 饰演了一个很是关键的脚色。

前面我们提到过，一个系统答应出现的能级 $E_n$ 称作能量的本征值(Eigen Value)。

现在，我们也响应地将这个饰演关键脚色的特解序列 $\phi_n(x)$ 称作能量的本征函数(Eigen Function)、大概叫做能量的本征态(Eigen State)。

这里对本征态的物理意义稍微多聊两句：

以能量本征态为例：一个粒子的波函数，凡是是能量本征态的线性叠加(即前面给出的级数和 )，这也是所谓“叠加态”，此时能量是不肯定的。但一旦我们去丈量它的能量时，波函数就会随机坍缩到其中一个本征态上，此时能量就是肯定的了。

所以，本征态的物理意义就是：对一个物理工具丈量某个力学量，获得某个肯定本征值的时辰，粒子所处的量子态。

打个不得当的比方：在薛定谔的猫的例子中，假如将“猫的死活”看成一个“力学量”(虽然这是虚拟的 )，那末“死猫”和“活猫”就是这个力学量的两个本征态。翻开盒子观察猫的死活之前，猫的状态就是两个本征态的叠加，但一旦翻开盒子看了猫以后，猫的状态就肯定了，此时它必定随机坍缩到某个本征态上，不是死就是活，绝对不会又死又活。

不外需要留意的是，当粒子处于能量的某个本征态 $\phi_n(x)$ 、即具有肯定的能量值 $E_n$ 时，位置仍然是不肯定的，此时位置的几率散布仍然由 $|\phi_n(x)|^2$ 计较。

而这个几率散布的一个直观的例子，就是原子核外各类形状的电子云，每一种电子云形状实在就对应了能量的一个本征态(正确说是三维情形下的 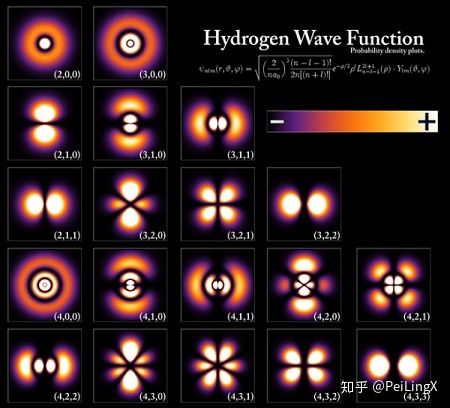$\phi_{nlm}(r,\theta,\varphi)$ )，这个我们今后再诠释：

而这个本征态的概念可以推行到肆意力学量：

对于一个具体的物理工具，肆意一个力学量 $F$ 城市对应一组答应取值的本征值 $F_n$ (也就是典范力学中可以被丈量到的值 )和响应的本征态 $f_n$ ，当我们将 $\psi$ 暗示成这些本征态的级数和 $\psi=\sum_n{k_nf_n}$ 时，响应的系数的模方 $|k_n|^2$ 就是测得该粒子 $F=F_n$ 的几率。

由此，我们就看到了波函数若何包括典范力学量的几率信息。

而在量子力学中，某个力学量的本征值和本征态信息，实在也完整描写了这个力学量自己，从这个意义上说，本征值和本征态就是“一个力学量的ID”。

那末，怎样才能找到一个力学量的本征值和本征态呢？

这将经过求解所谓的“本征方程”来实现。

接下来的题目自然就是：本征方程长什么样？

前面我们提到“本征值”时，在括号里备注了它的英文： Eigen Value，而这个词的另一其中文翻译，是线性代数中的“特征值”，这不由让我们浮想联翩：

也许本征方程和线性代数中的特征值理论有关？

我们这就回到线性代数中看看。

4) 叙旧：特征值与特征向量

在线性代数中，一个矩阵与向量相乘的进程，可以看成是对向量的某种操纵。

从成果上来说，一个“普通的”矩阵碰上一个“普通的”向量时，凡是会对这个向量发生一些扭转加伸缩的分解结果，而且在分歧的向量上会形成份歧的扭转角度和伸缩系数。

不外，对于一个矩阵而言，我们总是能找到一组“不普通的”向量，使得这个矩阵感化在上面时，只发生伸缩的结果，而不会使其扭转。

这样的向量，就是这个矩阵的特征向量，而它伸缩的比例，就是响应的特征值。

写成矩阵相乘的形式，就是：

$\bm A\bm\alpha=\lambda\bm\alpha$

其中 $\bm\alpha$ 是矩阵 $\bm A$ 的特征向量， $\lambda$ 是响应的特征值。

现在我们回到量子力学，来看看这个关系式的一个失散多年的孪生兄弟。

5) 本征方程

温馨提醒：以下内容能够由于过于笼统而引发不适。

量子力学中，一个力学量也会对应一个类似于矩阵的工具，我们将它称作“算符”，凡是是在该力学量的标记上加一个小尖帽 $\hat{}$ 。

比如，一个粒子的 $x$ 坐标有“ $x$ 坐标算符”，记作 $\hat{x}$ ；动量有动量算符，记作 $\hat{\bm p}$ 。

而我们最关注的能量，也有能量算符，又叫哈密顿算符(Hamiltonian Operator，这是由于典范力学中能量又被称作哈密顿量)，记作 $\hat{H}$

能否是很头疼？这好端真个，怎样又冒出一堆新玩意儿来。

但不管怎样样，来都来了，我们还是问问这堆算符的物理意义是什么吧。

零丁会商算符的物理意义是比力困难的，但我们可以像矩阵感化在特征向量上面一样，将一个算符、比如哈密顿算符 $\hat{H}$ 感化在它的某个本征态 $\phi_n$ 上面，形式上写成： $\hat{H}\phi_n$ ，这个时辰便可以会商物理意义了。

不严酷地说，这个式子的物理意义可以了解为，对一个处于状态 $\phi_n$ 的粒子丈量它的能量。

而按照前面提到的本征态的物理意义，我们晓得，此时我们会百分之百获得一个肯定的能量值 $E_n$ ，丈量竣事以后，粒子的状态仍然处于 $\phi_n$ 。

将这个物理进程写成一个关系式，就是：

$\hat{H}\phi_n=E_n\phi_n$

不严酷地说，这个公式的左侧可以了解为丈量行为，右侧可以了解为丈量成果。

而能量算符与能量本征态的这个关系，对于一般的力学量也建立，肆意一个力学量 $F$ 与它的本征态 $f_n$ 之间也满足：

$\hat{F}f_n=F_nf_n$

(其中 $F_n$ 是本征态 $f_n$ 对应的本征值 )

看，这个式子能否是和矩阵的特征向量关系式 $\bm A\bm\alpha=\lambda\bm\alpha$ 形式上很像？

没错，这就是我们要找的本征方程的笼统形式。

(可以看到，力学量算符感化在波函数上，形式上和矩阵感化在向量上一样，这就是为什么我们将波函数又称作“态矢量”的缘由 )

不外，这个笼统形式看起来虽然很有事理的样子，但还是不能当饭吃。究竟，我们拿着本征方程是要找出本征值和本征态的。

所以接下来，我们要来关注本征方程的具体计较。

现实上，假如晓得了力学量算符的氖亟谶体的、可以计较的形式，那末从理论上说，本征值和本征态便可以经过本征方程被解出来。

那末，这些算符的具体的形式长什么样呢？

在线性代数中，我们晓得，它们就是一个个具体的矩阵。

而在量子力学中，算符的花样会比力多：它们偶然辰表示成一个(无穷维的 )矩阵，偶然辰又是一个函数，甚至偶然辰还会酿成其他骨骼清奇的怪物……

我们还是以我们最关注的能量算符、也就是哈密顿算符 $\hat{H}$ 为例来具体看一看。

6) 能量的本征方程

我们先从形式上写出能量的本征方程：

$\hat{H}\phi_n=E_n\phi_n$

由于能量本征值 $E_n$ 即本征态 $\phi_n$ 都已经有了具体的值或函数形式，是以接下来的使命，就是要找出哈密顿算符的具体形式(坐标表象下 )。

这需要我们从牛顿力学中寻觅一些启迪。

在牛顿力学中，我们晓得，一个系统的总能量(单指机械能 )是动能与势能之和，即：

$E=E_k+E_p$

而动能： $E_k=\frac{1}{2}mv^2=\frac{p^2}{2m}$

因而： $E=\frac{p^2}{2m}+E_p$

这个关系式可以间接照搬到算符上面来，我们将动量算符记为 $\hat{p}$ 、势能算符记为 $\hat{E}_p$ ，那末我们可以形式上写出哈密顿算符(能量算符 )与动量、势能算符之间的关系：

$\hat{H}=\frac{\hat{p}^2}{2m}+\hat{E}_p$

之所以要写成这样的形式，是由于动量和势能两个算符的具体形式(坐标表象下 )是我们可以间接给出来的。

先说简单的：势能算符 $\hat{E}_p$ ，可以间接暗示成势能关于坐标的函数 $V(x)$

而动量算符 $\hat{p}$ (只会商一维情形 )，就是我们前面说的“骨骼清奇的怪物”的一个例子，它是一个微分算子：

$\hat{p}=-\text i\hbar\frac{\partial }{\partial x}$

(这个关系式的由来说来话长，这里不展开，还是在阿谁深度科普系列 从线性代数到量子力学 中，有一个不松散但相对易于了解的说明 )

将这两个式子代入哈密顿算符关系式中，得：

$\hat{H}=-\frac{\hbar^2}{2m}\frac{\partial ^2}{\partial x^2}+V(x)$

再将哈密顿算符代入能量本征方程中，我们就获得：

$\hat{H}\phi_n=-\frac{\hbar^2}{2m}\frac{\partial ^2\phi_n}{\partial x^2}+V\phi_n=E_n\phi_n$

由于本征函数 $\phi_n$ 只是 $x$ 的函数，是以上式中对坐标的偏导可以写成 ${\phi_n}''$ ，因而方程化为：

$-\frac{\hbar^2}{2m}{\phi_n}''+V\phi_n=E_n\phi_n$

还熟悉它吗？它就是我们前面分手变量获得的定态薛定谔方程！

7) 薛定谔方程的寄义

到这里，我们终究可以来理一理薛定谔方程的寄义了。

首先，适才我们已经看到，分手变量后获得的定态薛定谔方程，本质上就是能量本征方程的一个具体形式，它描写的是能量的哈密顿算符与能量本征值、本征态之间的关系。

这样一来，“求解薛定谔方程可以获得能量的本征值”这个结论从逻辑上说就没有什么违和感了。

现在我们再简单说说薛定谔方程本尊，虽然它对我们这个系列来说实在并不那末重要。

按照我们前面给出的哈密顿算符的关系式，我们可以将薛定谔方程写成笼统形式：

$\text i\hbar\frac{\partial }{\partial t}\psi=\hat{H}\psi$

从这个式子可以看出，它实在描写的是态矢量的时候演变纪律与系统能量之间的关系，大概说得更浅显一点，描写的是量子态的动力学纪律。

这也就是为什么我们经常将薛定谔方程比作“量子力学中的牛二定律”。

顺便提一句，这个演变纪律背后，还触及到一些更深条理的物理意义，不外这需要触及到分析力学、李群等离我们这个系列有些悠远的常识，我们就不继续深究了。

究竟，仅仅从适用主义的角度来说，我们实在只需要关必定态薛定谔方程就充足了。

8) 结语与预告

能将这篇烧脑文对峙读到最初的同学，你们真的不轻易。

说真话，实在文章写到最初，作者也不敢肯定，能否真的能对零根本的同学讲清楚薛定谔方程的寄义，究竟篇幅那末短、信息量那末多、而量子力学又那末笼统。

假如没有完全读懂文中内容，又想领会更多，可以看看文中一向安利的另一个深度科普系列：

阿谁系列更偏重于报告量子力学背后精巧的数学系统，节奏也比这篇文章慢很多，有爱好的同学可以去瞧瞧。

但不管有没有完全了解薛定谔方程，对于了解它的利用而言，我们只需要晓得一点就够了：

薛定谔方程能给出系统能量的本征态和本征值(也就是能级 )的信息，这是我们从第一性道理上了解化学元素的周期律和化学性质、了解材料的一些宏观物性、以及了解半导体道理的关键。

正是这个关键信息，带来了二十世纪光辉的物资文化。

接下来的几篇中，我们将见识到这一点。

20 个评论

游客 2022-2-27 22:01

大佬写的真好！！！！！！！

回复
游客 2022-2-27 22:00

老兄跟我一样不是物理专业的学生，不过一样对物理是真爱呀哈哈哈老兄写的真不错微观世界太迷人了，量子场论太不可思议了

回复
游客 2022-2-27 21:59

写的太好了为啥这么少赞呐

回复
游客 2022-2-27 21:59

针不戳，我懂了

回复
游客 2022-2-27 21:59

作为一个零基础的孩子表示较好地理解了薛定谔方程，感谢作者！！

回复
游客 2022-2-27 21:58

可别谦虚，学的时间不长，不一定就是初学者。给你点赞！

回复